Axe’s matching algorithm¶
Axe uses an algorithm based on longest-prefix-in-trie matching to match a variable length from the start of each read against a set of ‘mutated’ indexes.
Hamming distance matching¶
While for most applications in high-throughput sequencing hamming distances are a frowned-upon metric, it is typical for HTS read indexes to be designed to tolerate a certain level of hamming mismatches. Given these sequences are short and typically occur at the 5’ end of reads, insertions and deletions rarely need be considered, and the increased rate of assignment of reads with many errors is offset by the risk of falsely assigning indexes to an incorrect sample. In any case, reads with more than 1-2 sequencing errors in their first several bases are likely to be poor quality, and will simply be filtered out during downstream quality control.
Hamming mismatch tries¶
Typically, reads are matched to a set of indexes by calculating the hamming
distance between the index, and the first 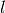 bases of a read for a
index of length
bases of a read for a
index of length 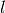 . The “correct” index is then selected by
recording either the index with the lowest hamming distance to the read
(competitive matching) or by simply accepting the first index with a hamming
distance below a certain threshold. These approaches are both very
computationally expensive, and can have lower accuracy than the algorithm I
propose. Additionally, implementations of these methods rarely handle indexes
of differing length and combinatorial indexing well, if at all.
. The “correct” index is then selected by
recording either the index with the lowest hamming distance to the read
(competitive matching) or by simply accepting the first index with a hamming
distance below a certain threshold. These approaches are both very
computationally expensive, and can have lower accuracy than the algorithm I
propose. Additionally, implementations of these methods rarely handle indexes
of differing length and combinatorial indexing well, if at all.
Central to Axe’s algorithm is the concept of hamming-mismatch tries. A trie is
a N-ary tree for an N letter alphabet. In the case of high-throughput
sequencing reads, we have the alphabet AGCT, corresponding to the four
nucleotides of DNA, plus N, used to represent ambiguous base calls. Instead
of matching each index to each read, we pre-calculate all allowable sequences
at each mismatch level, and store these in level-wise tries. For example, to
match to a hamming distance of 2, we create three tries: One containing all
indexes, verbatim, and two tries where every sequence within a hamming
distance of 1 and 2 of each index respectively. Hereafter, these tries are
referred to as the 0, 1 and 2-mm tries, for a hamming distance (mismatch) of
0, 1 and 2. Then, we find the longest prefix in each sequence read in the 0mm
trie. If this prefix is not a valid leaf in the 0mm trie, we find the longest
prefix in the 1mm trie, and so on for all tries in ascending order. If no
prefix of the read is a complete sequence in any trie, the read is assigned to
an “non-indexed” output file.
This algorithm ensures optimal index matching in many ways, but is also extremely fast. In situations with indexes of differing length, we ensure that the longest acceptable index at a given hamming distance is chosen; assuming that sequence is random after the index, the probability of false assignments using this method is low. We also ensure that short perfect matches are preferred to longer inexact matches, as we firstly only consider indexes with no error, then 1 error, and so on. This ensures that reads with indexes that are followed by random sequence that happens to inexactly match a longer index in the set are not falsely assigned to this longer index.
The speed of this algorithm is largely due to the constant time matching
algorithm with respect to the number of indexes to match. The time taken to
match each read is proportional instead to the length of the indexes, as for a
index of length 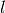 , at most
, at most 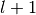 trie level descents are
required to find an entry in the trie. As this length is more-or-less constant
and small, the overall complexity of axe’s algorithm is
trie level descents are
required to find an entry in the trie. As this length is more-or-less constant
and small, the overall complexity of axe’s algorithm is 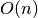 for
for
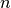 reads, as opposed to
reads, as opposed to 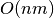 for
for 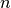 reads and
reads and 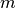 indexes as is typical for traditional matching algorithms
indexes as is typical for traditional matching algorithms